1. 生长与偏好连接和BA模型
针对上述第二个问题,1999年已经给出了回答,造成埃尔德什-雷尼模型不能够产生真实网络中的枢纽节点和幂律分布的原因在于,其两个假设条件违背了真实网络的性质。在真实网络中,网络通过添加新节点而不断增长,新增节点倾向于与链接数高的节点相连。然而在随机网络中,模型假设节点数目\(N\)是固定的。因此,在真实网络建模时,必须承认这样一个事实:即网络是一个增长过程的产物。此外,随机网络还假设节点随机选择其它节点进行连接。然而,真实网络中新加入节点更倾向于与连接数高的节点相连,这一过程被称为偏好连接。总之,无标度网络与随机网络之间两个重要的不同之处为(1) 生长,真实网络是一个生长过程,其节点数\(N\)会持续增加。而随机网络模型假设节点数目\(N\)是固定的。(2)偏好连接,真实网络中,新节点倾向于和链接数高的节点相连。相反,随机网络中的节点随机选择节点进行连接。
在认识到真实网络是由于节点增加和偏好连接共同作用的结果,那么就可以通过这两个条件构建一个可以生成幂律分布的网络生长模型,也即是巴拉巴西-阿尔伯特模型,也被称为BA模型,或无标度网络模型。该模型的定义如下:初始时,网络中有\(m_0\)个节点,这些节点之间任意连接,但需保证每个节点至少有一个链接即可,即要保证是连通的。随后网络按如下两个方面演变。(1) 每个时间步里,向网络中添加一个拥有\(m(\leqslant m_0)\)条链接的新节点,该节点会和网络中已经存在的\(m\)个节点相连。(2) 新节点选择度为\(k_i\)的节点进行连接的概率为\(\Pi(k_i)=k_i/\sum_j k_j\)。偏好连接是一个概率化的机制:新节点可以和网络中任意节点相连,无论对方是枢纽节点还是只有单个链接的节点。随机网络节点的增长,一些节点逐渐成长为枢纽节点,但大部分节点仍然是只有几个连接。这些枢纽节点就是“富者越富”现象的结果:偏好连接机制,使得新节点更倾向于与链接数高的节点相连。
2. 度动力学和度分布
为了探究无标度特性的涌现,接下来考察BA模型随机时间演变的过程。用一个实数来近似\(k_i\),该变量可理解为\(k_i\)在很多次网络生长过程中的平均值。那么节点\(i\)获得新连接的速率为:
\[\frac{dk_i}{dt}=m\Pi(k_i)=m\frac{k_i}{\sum_{j=1}^{N-1}k_j}\]此处,系数\(m\)体现的是每个新节点会带来\(m\)个链接。因此,节点\(i\)有\(m\)次被选择的机会。上述公式分母是关于网络中除新加入节点之外的所有节点进行的,因此有\(\sum_{j=1}^{N-1}k_j=2mt-m\)。从而上述公式可写为:
\[\frac{dk_i}{dt}=m\Pi(k_i)=\frac{k_i}{2t-1}\]当\(t\)比较大时,可忽略分母中\(-1\)项,进而得到:
\[\frac{dk_i}{k_i}=\frac{1}{2}\frac{dt}{t}\]考虑到\(k_i(t_i)=m\) (节点\(i\)在时刻\(t_i\)加入网络时拥有\(m\)个链接),对上述公式积分有
\[k_i(t)=m\left(\frac{t}{t_i}\right)^\beta\]称\(\beta\)为动态指数,取值为\(\beta=1/2\)。从而,根据上式可得如下推论:
(1) 每个节点的度都依照幂律增长,并且有相同的动态指数\(\beta=1/2\),因此所有节点都遵循相同的增长规律。
(2) 度的增长是亚线性的,每个新节点在加入网络时,都比在它之前加入网络的节点有更多的节点可以连接。因此,随着时间的积累,每个节点会与更多的节点竞争被连接的机会。
(3) 节点\(i\)越早加入网络,它的度\(k_i(t)\)就越高。因此,枢纽节点的度很高,是由于它比其它节点更早加入网络。
(4) 新节点\(i\)获得链接的速率为
\[\frac{dk_i(t)}{dt}=\frac{m}{2}\frac{1}{\sqrt {t_it}}\]这也就意味着在每个时间步,节点越老,获得的链接就越多。节点获得链接的速率随着时间下降\(t^{1/2}\)。随着时间推移,每个节点获得链接的数目会越来越少。
BA模型生成的网络有一个显著特征,即幂律度分布,那么度分布\(p_k\)的函数形式是什么,如何理解你形成的原因?通过连续介质理论,可得到度分布为
\[p(k)\approx2m^{1/\beta}k^{-\gamma}\]其中\(\gamma=1+1/\beta=3\),即度分布服从度指数为\(\gamma=3\)的幂律分布,其刻画了网络拓朴的量——度指数\(\gamma\)和刻画节点随时间演化的动态指数\(\beta\)联系在一起,揭示了网络拓朴和网络动力学之间的深层关系。上述公式的前置因子可通过主方程或速率方程方法得到,还可以使用线性化弦图模型精确计算得到其确切形式为:\[p_k=\frac{2m(m+1)}{k(k+1)(k+2)}\]这意味着
(1) 当\(k\)很大时,上述公式可简化为\(p_k\sim k^{-3}\),也即\(\gamma=3\);
(2) 度指数\(\gamma\)独立于\(m\);
(3) 度分布是独立于\(t\)和\(N\),因此,模型得到是一个稳定的无标度状态;
(4) 幂律分布的系数是正比于\(m(m+1)\)。
总之,度指数和模型参数\(m\)和\(m_0\)都无关,模型产生的度分布是稳定的。
3. 生长或偏好连接的缺失
由BA模型的产生的两个条件为生长和偏好连接并在,那么这两个条件对无标度特性的出现都是必要的吗?换句话说,就是只保留其中一个机制是否也能够生成一个无标度网络呢?下面讨论这个模型的两个极端情况:
(1) 模型A
此模型中仅保留网络的生长机制(要素A),去掉了偏好连接机制(要素B)。模型A从\(m_0\)个节点开始,按以下步骤深化:(a) 生长,在每个时间步,添加一个拥有\(m\)条链接的新节点,使之与网络中已经存在的\(m\)个节点相连。(b) 随机连接,一个新节点与一个度为\(k_i\)的节点的相连接的概率为:\(\Pi(k_i)=1/(m_0+t-1)\)。即\(\Pi(k_i)\)与节点的度\(k_i\)无关,表明新节点是随机选择节点进行连接的。
根据连续介质理论,\(k_i(t)\)随时间呈对数增长:
\[k_i(t)=m ln\left(e\frac{m_0+t-1}{m_0+t_i-1}\right)\]模型A所得度分布服从指数分布
\[p(k)=\frac{e}{m}exp\left(-\frac{k}{m}\right)\]指数函数比幂函数的衰减快得多,此时网络中很难出现枢纽节点。因此,缺少偏好连接的模型无法得到无标度特性和枢纽节点。
(2) 模型B
此模型中保留了偏好连接机制,而去掉了生长机制,模型B从\(N\)开始,按如下步骤演化:在每个时间步,随机选择一个节点,该节点与其他节点相连时,选择度为\(k_i\)的节点的概率按照偏好连接概率公式计算。由于\(\Pi(0)=0\),因此,假设\(k=0\)时,节点的度为\(k=1\),否则这些节点无法获得连接。此外,在此模型中,网络中的节点数目在网络演化过程中保持不变,而链接数随时间呈线性增长。因此,当\(t\)很大时,每个节点的度也随时间呈线性增长:
\(k_i(t)\approx\frac{2}{N}t\)。在早期,网络只有少数几个连接时,每个新链接会连接两个之前没有任何链接的节点。此时,模型B的演化与BA模型没有区别,即度分布服从幂律分布。然而\(p_k\)是不稳定的。当\(t\rightarrow N(N-1)/2\),网络变成为一个完全图,此时所有节点的度都是\(k_{max}=N-1\),此时有\(p_k=\delta(N-1)\)。
综上所述,缺少偏好连接机制的模型A会得一个稳定的指数分布,相反,缺少生长机制的模型B无法得到稳定的分布,最终网络收敛到一个完全图。
4. 测量偏好连接和非线性偏好连接
BA模型生成网络的无标度特性是由生长和偏好连接机制共同作用产生的,生长机制容易理解,那么如何理解真实网络的偏好连接机制呢?偏好连接依赖于以下两个假设:(1) 一个节点被连接的概率\(\Pi(k)\)取决于它的度\(k\),这与随机网络是截然不同,随机网络模型中的\(\Pi(k)\)与\(k\)无关;(2) \(\Pi(k)\)与\(k\)是线性关系。
第一种情况,我们知道每个节点加入网络中的时间,第二种情况,我们知道一个网络在相隔不远的两个时刻的结构。考虑第二中情况,第一个时刻记为\(t\),第二个时刻记为\(t+\Delta t\),假设节点\(i\)的度在这两个时刻发生了变化,变化量记为\(\Delta k_i=k_i(t+\Delta t)-k_i(t)\),由\(\Pi(k_i)=k_i/\sum_j k_j\)知其相对变化量\(\Delta k /\Delta t\)为:\(\Delta k_i / \Delta t \sim \Pi(k_i)\)。为减少其噪声的影响,必为测量其累积偏好连接函数:\(\pi(k)=\sum_{k_i=0}^{k}\Pi(k_i)\)。
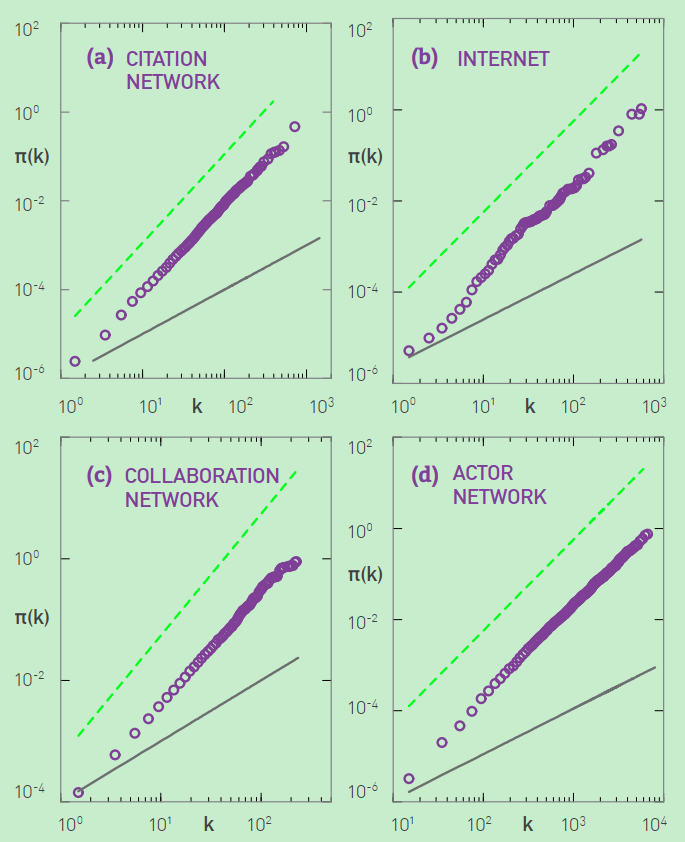
总之,偏好连接概率是依赖于节点的度,而且在有些系统中,偏好连接是线性的,在另外一些系统中偏好连接是亚线性的。
图1中观察到的亚线性偏好连接,引出一个重要的问题,即这种非线性的对网络结构有什么影响呢?基于上述非线性偏好连接,重新计算BA模型的度分布。当\(\alpha=0\)时,由于缺少偏好连接,此时BA模型退化为模型A,度分布服从指数分布。当\(\alpha=1\)时,模型等价于标准的BA模型,从而其度分布是服从幂律分布的。当\(\alpha \neq0\)和\(\alpha \neq1\)时,可发现以下种模式:
(1) 亚线性偏好连接\((0< \alpha <1)\)
此时,新节点倾向于和有较多链接的节点相连,但这种倾向是比较弱的,还不足以产生无标度的度分布。此时的度分布服从广延指数分布:
\[p_k\sim k^\alpha exp\left(\frac{-2\mu(\alpha)}{\langle k \rangle (1-\alpha)}k^{1-\alpha} \right)\]其中\(\mu(\alpha)\)仅弱依赖于\(\alpha\),上式的指数截断意味着,亚线性偏好连接限制了枢纽节点的大小和数量。同时亚线性偏好连接还会影响网络的最大度\(k_{max}\) 。对于亚线性偏好连接,有如下最大度\[k_{max}\sim (lnt)^{1/(1-\alpha)}\]这表明网络最大度的生长速度要远低于多项增长。也就是为什么\(\alpha<1\)时,枢纽节点要小一些的原因。
(2) 超线性偏好连接\((\alpha>1)\)
此时,新节点倾向于和大度节点相连的趋势增强了,加速了“富者愈富”的进程,当\(\alpha>2\)时,这一现象尤为显著,此时模型会出现“胜者能吃”的现象:几乎所有节点都连接到一个或几个超级枢纽节点。“胜者通吃”的现象也会影响最大枢纽节点的大小:\(k_{max}\sim t\)。因此,当\(\alpha >1\)时,最大枢纽节点和系统中有限的比例的节点相连。总之,非线性偏好连接会改变度分布,要么会限制枢纽节点的大小\((\alpha <1)\),要么会导致超级枢纽的产生\((\alpha >1)\)。因此,只有\(\Pi(k)\)是严格线性依赖于节点的度\(k\)时,所得到的网络才具有纯粹的幂律度分布。
5. 偏好连接的起源
一定会有人会问,偏好连接从那里来呢?一类人认为偏好连接是随机事件和网络结构性质之间相互作用的产物。这些信息不需要网络全局信息,仅依赖于随机事件,因此,称为局部或随机机制。另一类人认为每个新节点或新链接的形成都是平衡一些相互矛盾的需求,往往取决于成本利益分析。这类模型通常需要网络全局信息,且依赖于优先方法,因此,称之为全局优化机制。
(1) 局部机制
(a) 链接选择模型
定义如下:在每个时间步,向网络中添加一个新节点。随机选择一条链接,将新节点连接到所选链接其中一个端点上。此模型不需要全局拓朴信息,本质上属于局部和随机机制。一条随机选择的链接,其端点的度为\(k\)的概率为\(q_k=Ckp_k\),这个等式刻画两个效应,节点的度越高,就越容易成为随机选择链接的一端;网络中度为\(k\)的节点越多,这些节点越容易成为随机选择的链接的一端。该式中的常数\(C\)可以通过归一化条件\(\sum q_k=1\)得到,即\(C=1/\langle k\rangle\),因此一条随机选择的链接其端点的度为\(k\)的概率为:\[q_k=\frac{k p_k}{\langle k \rangle}\]表明概率\(q_k\)与\(k\)是线性关系。因此,链接选择模型通过产生偏好连接构造出了无标度网络。
(b) 复制模型
复制模型模拟了一个简单的形象,一个网页的作者倾向于从具有相关内容的其他网页中借鉴链接。该模型定义如下:在每个时间步,一个新节点加入网络中;随机选择一个节点\(u\),新节点以概率\(p\)连接到节点\(u\);以概率\(1-p\)随机选择节点\(u\)的一条出边,让新节点连接到这条边的另一端。节点\(u\)的随机选择的概率为\(1/N\),选择到度为\(k\)的节点概率为\(k/2L\),因此,新节点连接到度为\(k\)的节点的可能性为:
\[\Pi(k)=\frac{p}{N}+\frac{1-p}{2L}k\]可以看出,\(\Pi(k)\)和\(k\)是线性关系,对应着线性偏好连接。
综上所述,链接选择模型和复制模型都可以通过随机连接生产线性偏好连接。
(2) 优化模型
该模型假设所有节点都位于一个单位正方形中,每个时间步,添加一个节点,节点的位置在正方形内随机选择一个点来确定。新节点\(i\)选择节点进行连接时,成本函数为:\(C_i=min_j[\delta d_{ij}+h_j]\)。成本函数需要考察网络中存在的每个节点,\(d_{ij}\)为节点\(i\)和节点\(j\)之间的欧氏距离,\(h_j\)是节点\(j\)和“网络中心”之间的“网络距离”。把每个加入网络中的节点称为“网络中心”,认为其具有最好的网络性能。因此,\(h_j\)刻画了节点能够提供的资源,可用它和网络中心之间的距离来度量。由成本函数可得到三种不同的网络结构:
(a) 星型网络\((\delta<(1/2)^{1/2})\),当\(\delta=0\)时,欧氏距离不起作用,此时,每个节点都和网络中心直接相连,形成星型网络。实际上,只要\(h_j\)相对于\(\delta d_{ij}\)而言起主导作用,就会得到一个星型网络。
(b) 随机网络\((\delta \geqslant N^{1/2})\),当\(\delta\)较大时,\(\delta d_{ij}\)的贡献远大于\(h_j\), 此时,每个新加入的节点都会选择与其欧氏距离最近的节点相连,最终形成的网络的度分布是有界的,类似于随机网络。
(c) 无标度网络\((4\leqslant\delta \leqslant N^{1/2})\),此时网络具有无标度网络结构。
在优化模型中,幂律起源于两种相互竞争的机制:优化,每个节点都有一个吸引域,落在该节点吸引域的节点会和它相连,每个吸引域的大小和处于域中心的节点\(j\)的\(h_j\)有关。随机,随机选择新节点的位置,落在\(N\)个吸引域之中的某一个,已有节点中,度最大的节点具有最大的吸引域,因此会吸引最多的新节点,得到最多的新链接,最终形成偏好连接。
总之,产生偏好连接的微观机制有两种截然不同的起源。线性偏好连接既可以源自理性选择,也可以源自随机行为。
6. 直径与集聚系数
这里还有两个能够刻画BA模型的指标,即网络直径和集聚系数。
(1) 网络直径,表示网络中节点间的最大距离。当\(m>1\),并且\(N\)较大时,网络直径为:\[\langle d \rangle \sim \frac{lnN}{lnlnN}\]因此,网络的直径增长增长要比\(lnN\)慢很多。也即表示无标度网络的直径比同等大小随机网络的直径小,当\(N\)较大时,这一差距更为明显。
(2) 集聚系数,BA模型的集聚系数为:
\[\langle C \rangle \sim \frac{(lnN)^2}{N}\]该公式与随机网络中集聚系数对\(1/N\)的依赖关系大不相同。差异来源于\((lnN)^2\),在\(N\)较大时,这一项大大增加了集聚系数。因此,无标度网络中的集聚系数比随机网络中的集聚系数要高。
参考文献:
[1] 沈华伟,黄俊铭. 巴拉巴西网络科学[M]. 河南科学技术出版社,2020.

