本篇博客是关于徐晓伟老师*的讲课（数据管理新技术）笔记——Clustering. 主要包括K-means和DBCAN算法。
定义：
Grouping objects into sub-groups (clusters) # 等于对数据进行归纳，比如100万数据分成若干组，看不同自己的情况
such that:

• similar objects form a cluster
• dissimilar objects belong to different clusterts
• typically: a similarity-functoin distance is used to measure similarity between objects.

Basic operation for KDD and DataMining stand-alone application： summarize a large dataset.
focus further analysis (数据预处理): reduce a large data set by selecting only special clusters.
input for other data mining algorithms: characterize the propertises of the clusters and their relations

Application(目前应用十分广泛):

• customer segmentation (市场营销客户分组)
• document or image collections （图像或文档按相似度分组）
• web access patterns

分类：

• hierarchical clustering algorithms (分级聚类) – find successive clusters using previously established clusters
• partitioning clustering algorithms （普通聚类）- determine all clusters at once
• density-based clstering algorithms （基于密度的聚类）- determine clusters based on density （相同的数据属于同一个聚类，那么应该属于同一个密度比较大区域）

分级聚类的方法：
Aim to detect hierarchical relationships fo clusters by iteratively 不仅找到类，还要找到聚类的从属关系。

• 合并的：merging clusters (agglomerative) 聚类，假设10万个，合并5万个，再合并为1000个，可以用树来表示，根节点表示最大的聚类。
• 分裂的：splitting clusters (divisive)，所有的数据都属于一个类，树根，按相似度分为几个小的类，每个叶节点都只有一个数据。

A similarity measure of clusters is needed.
minimum distance between elements of each cluster (also called single linkage clustering): $\min{ { d(x,y): x \in A, y \in B } }$

maximum distance between elements of each cluster (also called copmplete linkage clustering ) : $\max {d(x,y):x\in A, y \in B }$
mean distance between elements of each cluster (also called average linkage clustering): $\frac{1}{|A| |B|} \sum_{x \in A} \sum_{y \in B} d(x, y)$
Running time $O(n^2)$
Difficult to determine the cut of dendrogram


$K$-means Clustering Method
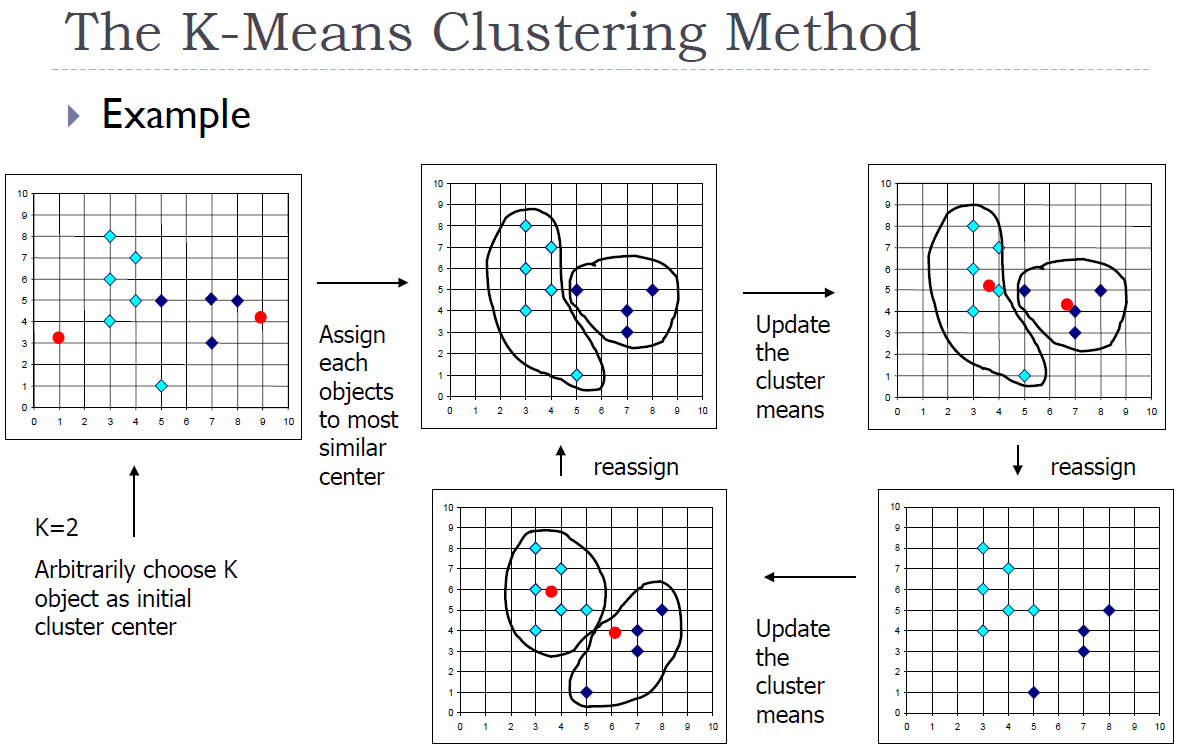
Given $k$, the k-means algorithm is implemented in four steps:

1. Partition objects into $k$ nonempty subsets; (初始化，随机分类)
2. Compute seed points as the centroids of the clusters fo the current partition (the coentrolid is the center i.e., mean point of the cluster); (算质心：坐标求和取平均)
3. Assign each objects to the cluster with the nearest seed point ; (每个类到质心的距离)
4. Go back to step 2, stop when no more new assignment; （整个过程反复迭代）

如果不知道 $k$,需要反复的试。过程是收敛的，每个点到中心的距离越变越小，下限不能小于 $0$.
每次循环做 $k * n$ 次比较，算质心：坐标的和求平均。$O(kn + k)$,到底循环多少次，根据数据的分布有关系，不能直接算 $O(tnk)$

可视化演示：https://www.naftaliharris.com/blog/visualizing-k-means-clustering/

课堂提问：
几个参数？
1. 质心在变 （固定参数，1先固定质心，解优化过程中，怎样分配，让目标函数降低，每个点到质心的距离总和是目标函数，每个距离都极小化，一个k个质心，让每个数据都找到一个最近的质心。）
2. 从属关系在变 （同时解这两个参数很难，所以固定一个，再解一个，叫EM方法，第一步估计(Expection)，第二步是目标最大化 maximization，得到最优解之后更新另个）


基于密度的聚类方法：
Clusterr are sense regions in the data space, separated by regions of lower objects density.

Adcantages:

• Clusters can have arbitrary shape and size （k-means 只能找到规则形状的类，基于密度的聚类可以不受限于形状，大小可调）
• Number of clusters is determined automatically (不需要k超参数？啥叫超参数)
• Can separate clusters from surrounding noise （区分噪声点和非噪声点）
• Can be implemented efficiently （很高效）
• Can be integrated into databases （对数据库支持很好）

e-neighborhood of q, $Ne(q) = {p \in D | dist(q,p) <= e}$
r core object w.r.t. $\delta, MinPts if |Ne(q) >= MinPts|$

MinPts 表示参数，例如=5，如果一个区域内点的个数大于 5， 就叫做直接可达。

p directly density-reachable from q w.r.t. e MinPts, if 
$p \in N_\delta (q)$ and 
$q$ is a core object w.r.t. $\delta$ , MinPts.

density-reachable: = transitice closure

Cluster:
 maximal w.r.t. density reachability
any two points are density – connected
i.e., density-reachable from a third object 

noise : any object not contained in a cluster

DBSCAN Algorithm

e (半径), MinPts(圈圈包含多少个点才行)

任意选一个数据，以它为中心，画圈圈，以e为半径，在高维空间就是个超球。但是这个圈圈里只有一个1个，小于 MinPts, 所以不是核心点。
随便找下一个点，同样画一个圈圈，数点，发现这次有3个点，直接可达的。类的定义：必须是极大化的，所有其他点，能不能以两个绿颜色的点为中心，画圈圈，数点，重复刚才的工作，继续扩大。 没有新的点加入，找另个，这回有两个新的绿颜色点，这回两个绿颜色和三个红颜色的点是属于同一个类的。这次再看能不能抓一些新的数据进来。如果一直有新的，就一个画，没有了就停了。

算法复杂度：
画圈，看圈里有多少数据，n 个向量，n 个圈圈，复杂度为 O(n)。
O(n * runtime (e –neighborhood query))
regionquery * algorithm
Without inde $O(n)$ $O(n^2)$
With index $O(log(n))$, $O(n*log(n))$
CLARANS on SEQUOIA 2000 data

DBSCAN的演示：https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/


估计参数的方法请参考原文

• Ester M, Kriegel H P, Sander J, et al. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise[C]// International Conference on Knowledge Discovery & Data Mining. 1996.

DBSCAN算法下载：http://www.cs.ecu.edu/dingq/CSCI6905/readings/DBSCAN.pdf
DBSCAN算法也有不足：

而此时k-means算法效果反而更好？

** libsvm.zip已上传至资料，传送门：https://www.neusncp.com/user/file?id=156
另附斯坦福大学数据挖掘课程的PPT一份：12-clustering.pdf
————————
* 徐晓伟，美国阿肯色大学小石城分校信息科学系教授，兼任数学系教授；曾任美国联邦食品和药物管理局国家毒理学实验室（National教授。1983年在南开大学数学系获得学士学位，1987年在中国科学院沈阳计算技术研究所获得硕士学位，1998年在德国慕尼黑大学（University of Munich）获得博士学位。1998年~2002年在西门子公司任高级研究科学家； 自2012年任中国科学院沈阳自动化研究所客座研究员，博士生导师; 同时兼任东北大学客座教授。曾经是香港中文大学访问教授；为多家国际公司提供咨询服务，其中包括西门子公司，Axciom 公司，Dataminr 公司 和东软公司。多次在模式识别和数据挖掘领域知名国际会议上作大会特邀报告，在国际知名学术期刊和国际会议上发表了具有原创性的研究成果。他提出的基于密度的聚类等一系列理论算法，具有理论原创性，并被写入教科书。
** NEUSNCP平台注册免邀请码注册链接： Click